
If you arrange the coordinate system instead such that the downwards direction is positive, then acceleration due to gravity takes a positive value.) Because gravity is vertical,Ī x = 0 a x = 0. (Note that this definition assumes that the upwards direction is defined as the positive direction. The components of acceleration are then very simple:Ī y = – g = – 9.80 m /s 2 a y = – g = – 9.80 m /s 2. We will assume all forces except gravity (such as air resistance and friction, for example) are negligible. We must find their components along the x- and y-axes, too. Of course, to describe motion we must deal with velocity and acceleration, as well as with displacement. However, to simplify the notation, we will simply represent the component vectors as x x and y y.) If we continued this format, we would call displacement s s with components s x s x and s y s y. (Note that in the last section we used the notation A A to represent a vector with components A x A x and A y A y.

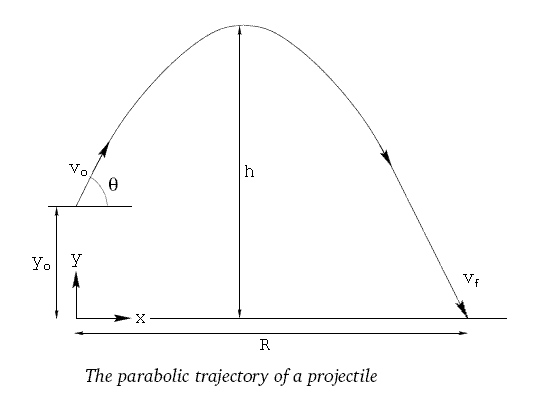
The magnitudes of these vectors are s, x, and y. Figure 3.34 illustrates the notation for displacement, where s s is defined to be the total displacement and x x and y y are its components along the horizontal and vertical axes, respectively. (This choice of axes is the most sensible, because acceleration due to gravity is vertical-thus, there will be no acceleration along the horizontal axis when air resistance is negligible.) As is customary, we call the horizontal axis the x-axis and the vertical axis the y-axis. The key to analyzing two-dimensional projectile motion is to break it into two motions, one along the horizontal axis and the other along the vertical. This fact was discussed in Kinematics in Two Dimensions: An Introduction, where vertical and horizontal motions were seen to be independent. The most important fact to remember here is that motions along perpendicular axes are independent and thus can be analyzed separately. In this section, we consider two-dimensional projectile motion, such as that of a football or other object for which air resistance is negligible. The motion of falling objects, as covered in Problem-Solving Basics for One-Dimensional Kinematics, is a simple one-dimensional type of projectile motion in which there is no horizontal movement. The object is called a projectile, and its path is called its trajectory. Projectile motion is the motion of an object thrown or projected into the air, subject to only the acceleration of gravity. Apply the principle of independence of motion to solve projectile motion problems.Determine the location and velocity of a projectile at different points in its trajectory.

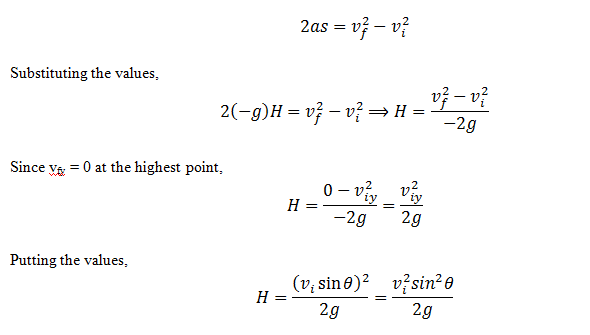
These are the same calculations that the "regular" formulas come from,Įxcept that the "up" and "down" parts are not equal.Īlternatively, you can use your formula for height.
#Projectile motion calculator unknown initial height plus#
The total flight time is the time going up plus the time going down.ĭuring the total flight time, the projectile continues moving at the same horizontal velocity. You also compute the height at the top of the trajectory (initial height plus height gained during the time you just calculated).įrom the height at the top of the trajectory, and the height of the impact area (I'm guessing this is zero for your problem, since you only said the initial height was not zero), you compute the amount of time spent falling. (That is, we pretend the Earth is flat and non-rotating.)Īssuming the initial firing direction is at some upward angle, you have an initial upward velocity component and an initial forward velocity component.įrom the initial height and upward velocity you compute the time until the top of the trajectory, when the projectile has zero vertical velocity. I'll make the usual first-year physics assumptions that there is no air resistance and no effects from the curvature of the Earth or from the Earth's rotation.


 0 kommentar(er)
0 kommentar(er)
